Jack-0810
2018-05-30 14:19
众测君，至今十以内的加减法都要愣半天。不错啦，俺十以内的数字没几个认识！[捂脸]
尽管高考那年数学满分，可我依旧认为数学是最难的一门课程！
打个比方：如果把人类所获得的知识比作一个圆，圆内的区域表示已知的知识，那么圆外的区域则是未知的世界！圆是你目前所掌握的。
很显然，未知的领域有多大！有多可怕！而数学恰恰反映了这一状况！
世界三大数学猜想：费马猜想、四色猜想和哥德巴赫猜想。
▲费马猜想：
当整数n > 2时，关于X、Y、Z的不定方程 x^n + y^n = z^n 无正整数解。
费马：法国数学家(被誉为业余数学家之王)！
其证明于1994年由英国数学家安德鲁·怀尔斯(Andrew Wiles)完成，遂称费马大定理！
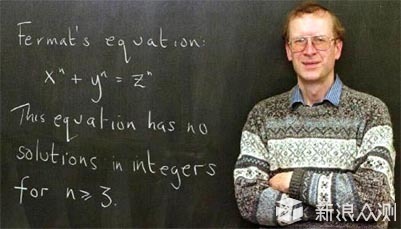
费马大定理，又被称为“费马最后的定理”，由法国数学家费马提出。它证明当整数n>2时，关于X、Y、Z的不等式公式XN +YN ≠ ZN 成立。费马大定理被提出后，经历多人猜想辩证，历经三百多年的历史。德国佛尔夫斯克宣布以10万马克作为奖金奖给在他逝世后一百年内，第一个证明该定理的人，吸引了不少人尝试并递交他们的“证明”。在一战之后，马克大幅贬值，但该定理的魅力并没有下降，证明费马大定理的人越来越多了。
▲四色猜想：
任何一张平面地图只用四种颜色就能使具有共同边界的国家着上不同的颜色。
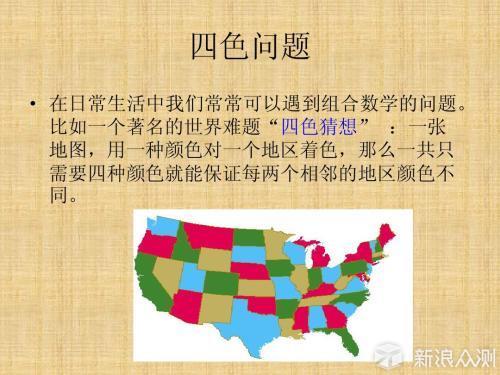
用数学语言表示，即“将平面任意地细分为不相重叠的区域，每一个区域总可以用1，2，3，4这四个数字之一来标记，而不会使相邻的两个区域得到相同的数字。”
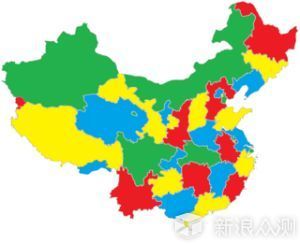
其证明于1976年由美国数学家阿佩尔(Kenneth Appel)与哈肯(Wolfgang Haken)借助计算机完成，遂称四色定理！
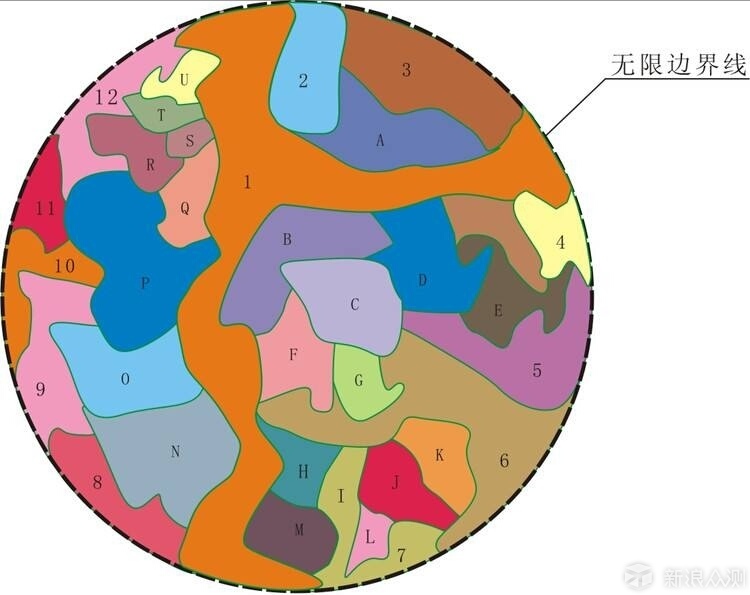
▲哥德巴赫猜想：
任一大于2的偶数都可写成两个质数之和。
(猜想手稿)
但是哥德巴赫自己无法证明它，于是就写信请教赫赫有名的大数学家欧拉帮忙证明，但是一直到死，欧拉也无法证明。
目前最好的成果(陈氏定理)乃于1966年由中国数学家陈景润取得。
经历：1920年，挪威数学家布朗证明了定理“9+9”，由此划定了进攻“哥德巴赫猜想”的“大包围圈”。这个“9+9”是怎么回事呢？所谓“9+9”，翻译成数学语言就是：“任何一个足够大的偶数，都可以表示成其它两个数之和，而这两个数中的每个数，都是9个奇质数之积。” 从这个“9+9”开始，全世界的数学家集中力量“缩小包围圈”，当然最后的目标就是“1+1”了。
1966年，中国著名数学家陈景润攻克了“1+2”，也就是：“任何一个足够大的偶数，都可以表示成两个数之和，而这两个数中的一个就是奇质数，另一个则是两个奇质数的积。”这个定理被世界数学界称为“陈氏定理”。
由于陈景润的贡献，人类距离哥德巴赫猜想的最后结果“1+1”仅有一步之遥了。但为了实现这最后的一步，也许还要历经一个漫长的探索过程。有许多数学家认为，要想证明“1+1”，必须通过创造新的数学方法，以往的路很可能都是走不通的。
本文来自热门话题任务-《哪一门课难到你吐血》精选用户作业。
关注官方微博 微博
关注官方微信
Copyright © 1996-2024 SINA Corporation, All Rights Reserved 新浪公司 版权所有
